
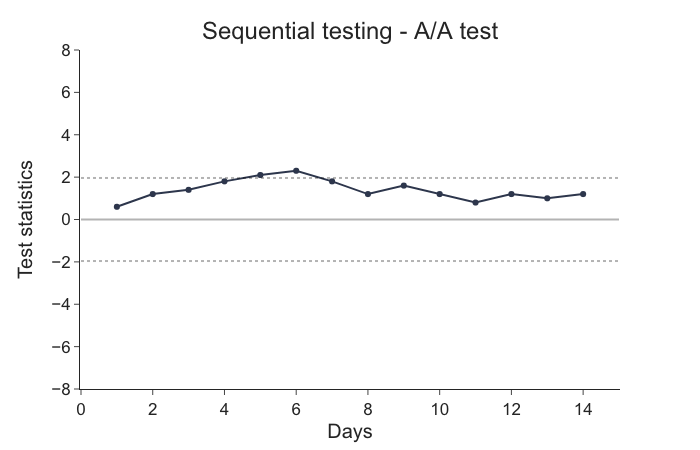
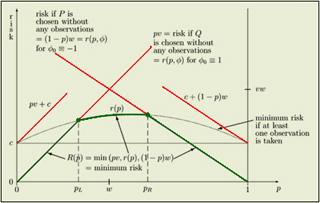
Sequential estimation is also discussed (Section 5). The development of sequential methods has been much stimulated by the sequential probability ratio test introduced by Abraham Wald, and discussion of procedures based on this test occupies the major part of this survey (Section 3). "Sequential Analysis" is taken to include all those investigational procedures in which the final pattern of observations is not determined before the start of the investigation, but depends, in some specified way, on the data collected in the course of the investigation. Numerical solutions for some frequently encountered special cases are developed and are compared with the results of Monte Carlo simulations. Unfortunately, they have nonunique solutions in the general case except for the truncated SPRT. These inductive equations provide a theoretical foundation for performance analysis. In this article, inductive integral equations governing these functions are developed under very general settings-the bounds can be time-varying and the LLRs are assumed independent but nonstationary. These functions have been studied extensively under the assumption of independent and identically distributed log-likelihood ratios (LLRs) with constant bounds, which is too stringent for many applications. The performance of SPRT is characterized by two important functions-operating characteristic (OC) and average sample number (ASN), and CUSUM's performance is revealed by the average run length (ARL) function. It forms the basis of numerous sequential techniques for different applications for example, the truncated SPRT and Page's cumulative sum test (CUSUM). The sequential probability ratio test (SPRT) is a fundamental tool for sequential analysis.


 0 kommentar(er)
0 kommentar(er)
